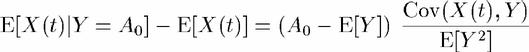Quantitative Predictions
D. Sornette
Passion for interdisciplinary work
- Economics (M. Aoki, T. Lux, P. Santa-Clara, D. Zajdenweber…)
- Cognitive science, neuro-economics, evolutionary psychology (R. Boyd, A. Fiske, R. Dunbar, J. Satinover…)
- Biology and medecine (biomembranes, parturition, critical illness, immune system collapse)
- Material and engineering failure
- Geophysics (earthquakes, landslides, space weather…)
- Physics and mathematics of complex systems, self-organization
Strong experience and taste for collaboration with Industry
(EADS, Thales, Eurocopter, reinsurance (Bermuda), banks, …)
Strong international network of close collaborators
Teaching
(9 completed PhD's and 17 post-docs)
Extreme Events
- dramatic and rapid change of a system which is the culmination of a complex preparatory stage.
- fundamental societal impacts
- large natural catastrophes
- earthquakes,
- volcanic eruptions,
- hurricanes and tornadoes,
- landslides, avalanches,
- lightning strikes,
- meteorite/asteroid impacts,
- catastrophic events of environmental degradation.
- failure of engineering structures
- crashes in the stock market
- social unrest leading to large-scale strikes and upheaval
- economic drawdowns on national and global scales
- regional power blackouts
- traffic gridlock
- diseases and epidemics, etc.
- innovations
- economic returns of R&D
- Outlier - "king" - "black swan"
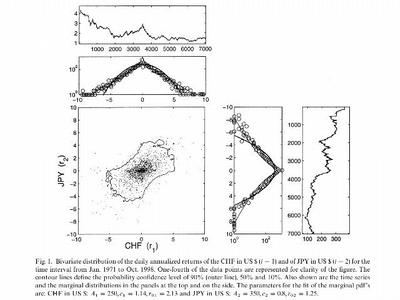
- Pdf of financial returns vs. drawdowns
- Positive feedbacks and finite-time singularities
- Population, GDP, financial indices…
- Mountain collapse
- Discrete scale invariance (hierarchies)
- Applications: PREDICTION
- Material rupture
- Financial bubbles and crashes
- Commercial sales

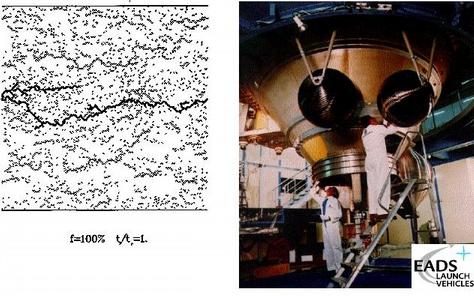
Material Damage and Failure
Our prediction system is now used in the industrial phase as the standard testing procedure.
J.-C. Anifrani, C. Le Floc'h, D. Sornette and B. Souillard "Universal Log-periodic correction to renormalization group scaling for rupture stress prediction from acoustic emissions", J.Phys.I France 5, n°6, 631-638 (1995)
Landslide Earthquakes
A landslide after the earthquake in El Salvador on 13th January 2001. In Santa Tecla (photo) 500 houses were buried, and 800 people were reported missing. The devastating quake triggered more than 10,000 landslides and damaged about 200,000 houses.
S. Helmstetter, D. Sornette, J.-R. Grasso, J. V. Andersen, S. Gluzman and V. Pisarenko, Slider-Block Friction Model for Landslides: Application to Vaiont and La Clapiere Landslides, J. Geophys. Res., 109, B02409, doi:10.1029/2002JB002160 (2004).
D. Sornette, A. Helmstetter, J.V. Andersen, S. Gluzman, J.-R. Grasso and V.F. Pisarenko, Towards Landslide Predictions: Two Case Studies. Physica A 338, 605-632 (2004)

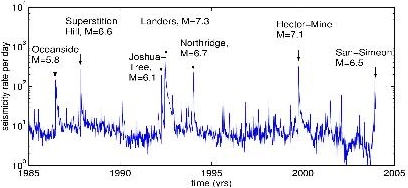
Deep connection with financial volatility
D. Sornette and G. Ouillon, Multifractal Scaling of Thermally-Activated Rupture Processes, Phys. Rev. Lett. 94, 038501 (2005)
G. Ouillon and D. Sornette, Magnitude-Dependent Omori Law: Theory and Empirical Study, J. Geophys. Res., 110, B04306, doi:10.1029/2004JB003311 (2005).
Self-organization versus "Catastrophism"
- Self-organization?
Extreme events are just part of the tail of power law distribution due to “self-organized criticality”? (endogenous) - “Catastrophism”: extreme events require extreme causes that lie outside the system (exogenous)
- A mixture? How would it work?
Guidelines from Physics: perturb and study the response
Linear Response Theory
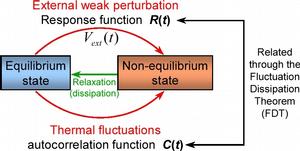
Problems:
- Externally imposed perturbations may be different from spontaneous fluctuations (external fluctuations lie outside the complex attractor)
- Attractor of dynamics may exhibit bifurcations
Endogenous versus Exogenous

The inspiration
- On Friday January 17, 2003, Sornette’s recent book jumped to rank 5 on Amazon.com’s sales ranking (with Harry Potter as #1!!!)
- Two days before: release of an interview on MSNBC’s MoneyCentral website
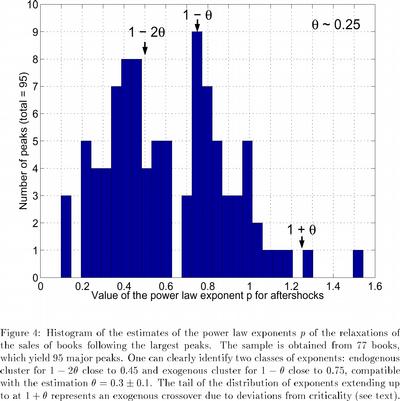
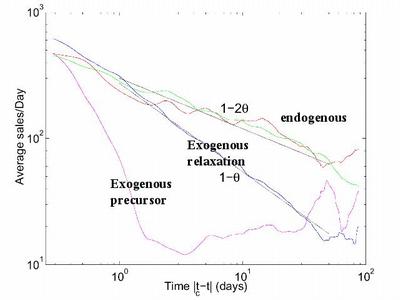
Two Kinds of Sales Peaks
D. Sornette et al., Phys. Rev. Letts. 93 (22), 228701 (2004)
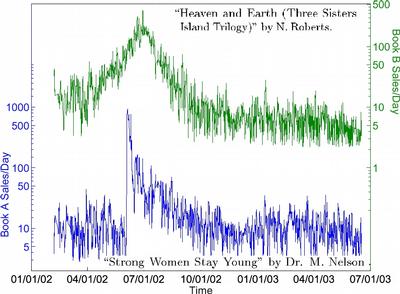
Exogenous versus Endogenous Shock
Exogenous shock
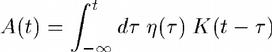
Exogenous shock
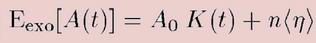
Endogenous Shock
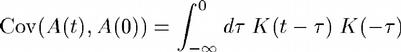
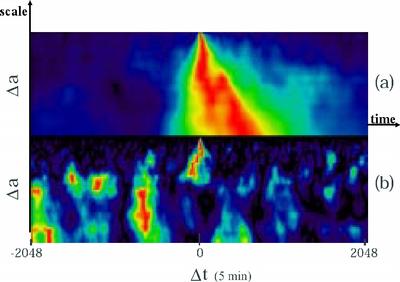
Causal cascade of volatility from large to small time scales
Arneodo, Muzy and Sornette (1998)
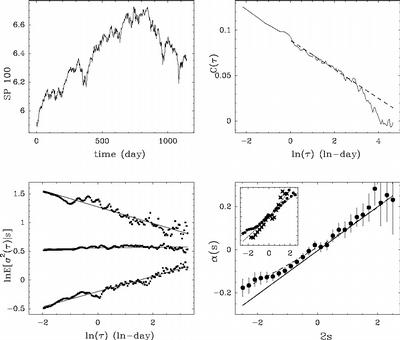
Financial Volatility
Relaxation of financial volatility
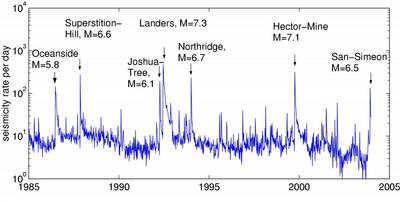
Deep connection between earthquakes and financial volatility

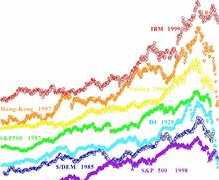
Various Bubbles and Crashes
Each bubble has been rescaled vertically and translated to end at the time of the crash


Patterns of price trajectory during 0.5-1 year before each peak: Log-periodic power law
Crashes as critical points of emergent instabilities
- A crash is the rupture ending a slow progressive maturation of a “bubble” toward an instability.
- Bubbles are unsustainable and die.
- Their death leads to change of regime, 2/3 of the time, this is a crash.
- 1/3 of the time, the bubble lands softly.
- Finite probability for a crash not to occur, given a bubble exists.
- It is rational for investors to stay in the market and pocket the exceptional returns, which remunerate them for the risk of the crash.

Higher-Moments portfolio theory and Copulas
- Gaussianization of multivariate distributions
- Copulas
- Test of the Gaussian copula hypothesis
- Why higher-order moments and cumulants
- Have your cake and eat it too!
- Generalized efficient frontiers
- Tail equivalence and asymptotic VaR
- Extreme conditional dependence measures
- Tail dependence for factor models